10 minutes
Wizard (card game)
Wizard is a fun card game played with a deck of 60 cards, consisting of a regular set of 52 playing cards and 4 Wizards and 4 Jesters.
Rules of the game per Wikipedia:
The objective of the game is to bid correctly on the number of tricks that a player will take in the subsequent round of play. Points are awarded for a correct bid and subtracted for an incorrect bid. The player with most points after all rounds have been played is the winner. The game is played in a number of rounds from 10 to 20, depending on the number of players and each round consists of three stages: Dealing, Bidding, and Playing. In the first round every player gets one card. In the subsequent rounds the number of cards is increased by one until all cards are distributed. That means that three players play 20 rounds, four players 15 rounds, five players 12 rounds and six players 10 rounds. The top card of the remaining cards is turned over to determine the trump suit. If there are no cards left or a jester is turned, there is no trump suit, and only the wizards are trump. If a wizard is turned, the dealer picks a trump suit. After looking at their cards, starting with the player to the dealer's left, each player states how many tricks he believes he will take, from zero to the number of cards dealt. This is recorded on a score pad. The player to the left of the dealer plays a card, and then the others follow clockwise. If a card other than a wizard or jester is played, the players have to follow suit, but it is possible to play a jester or wizard although the player has the desired suit. The Wizard beats all other cards but the first one in a trick beats all others. The jester is beaten by all others, but if all cards in a trick are jesters the first one beats the others. If a jester is played as the first card the first suit card decides which suit has to be followed. If a wizard is played as the first card every player is free to play what they want regardless of the others. If the first card is a Jester and the second a Wizard, then the Wizard rule takes precedence and players are not required to follow suit. At the end of each round, each player is given a score based on their performance. For predicting the number of tricks taken correctly, a player receives 20 points plus 10 points for each trick taken. For predicting the number of tricks taken incorrectly, a player loses 10 points for each trick over or under.
In the first round of the game of Wizard, each player is dealt only one card. Which means there is no "skill" of "choice" in the way each player will play their card and the round becomes a game of pure probability (almost... see Note [1]). In this post, we will simulate the first round of the game of Wizard and compute the probabilities of winning associated with each hand.
Note [1]: if the card flipped by the dealer is a Wizard, then the dealer will choose the trump suit. In the simulations below, I assume the trump suit is chosen randomly but I ran other simluations where the dealer chooses the trump suit that matches the card he has (as an example). Final probablities found barely changed.
First, let's create a deck of cards:
# Create deck of cards
# To make our life easier, we assume 11 = Jack, 12 = Queen, 13 = King and 14 = Ace
suits = ["H","D","C","S"] # for Hearts, Diamonds, Clubs and Spades
deck = [f"{n}-{s}" for n in range(2,15) for s in suits]
for _ in range(4):
deck.append("W") # Wizard
deck.append("J") # Jester
assert len(deck) == 60, "Deck has wrong number of cards"Simulate the first round of the game:
import random
def play_game(n_players):
"""
Plays Round 1 of a game of Wizard (players are dealt 1 card)
Returns
-------
winner: int
The winner of the round: an integer between [0, n_players - 1]
trump_card: str
A letter in ["H","D","C","S"] which determines the suit
player_cards: List[str]
The cards from each player
"""
# Shuffle the deck
random.shuffle(deck)
player_cards = deck[:n_players]
# One card is flipped to determine Trump card
trump_card = deck[n_players]
if trump_card == "J": # no trump card
trump_card = None
elif trump_card == "W": # dealer chooses trump card
trump_card = random.choice(["H","D","C","S"]) # assume the dealer chooses the trump card randomly
else:
trump_card = trump_card.split("-")[1] # Extract the suit from the card to assign the trump card
# if all cards dealt are Jesters
if all(card == "J" for card in player_cards):
return 0, trump_card, player_cards
# find first card not a Jester which determines the suit for the round
player_0 = 0
while player_cards[player_0] == "J":
player_0 += 1
if player_cards[player_0] == "W": # first player who has a Wizard wins the round
return player_0, trump_card, player_cards
else:
n0, s0 = player_cards[player_0].split("-")
n0 = int(n0)
winner = player_0
winner_n, winner_s = n0, s0
for player_id in range(player_0 + 1, n_players):
if "-" in player_cards[player_id]:
n, s = player_cards[player_id].split("-")
n = int(n)
if s == winner_s and n > winner_n: # same suit but better card
winner = player_id
winner_n, winner_s = n, s
elif winner_s != trump_card and s == trump_card: # trump card
winner = player_id
winner_n, winner_s = n, s
elif player_cards[player_id] == "W": # first player who has a Wizard wins the round
winner = player_id
break
return winner, trump_card, player_cardsThe goal is to find the probablity of winning for each card and each player.
We need to distinguish whether the card held by a player is a trump card or not (based on the card flipped by the dealer). We adopt the following notation:
- If the player holds a 5 of Hearts and Hearts is NOT the trump suit, we will call the card
5. - If the player holds a 5 of Hearts and Hearts IS the trump suit, we will call the card
T5. - If the player holds a 5 of Hearts and there are no trump suit (Jester flipped by the dealer), we will call the card
J5. Also, to make our life easier, we assume 11 = Jack, 12 = Queen, 13 = King and 14 = Ace. SoT13in the table below means you are holding the King in the trump suit.
We call the position of the player where the player is located in the round. Meaning if the player is the first player to announce his bet (and thus to play in the round), he will be in 1st position.
The probabilities of winning also depend on the number of players. The game consists of 3 to 6 players so we will run all the simulations.
Now let's run a Monte Carlo simulation of 1,000,000 games!
import numpy as np
import pandas as pd
n_players = 3 # between [3, 6]
n_games = 1000000
random.seed(124)
# Build a stats dictionary mapping a player's card with a list of wins/losses
stats = {}
cards = [str(s) for s in range(2, 15)] + ['T'+str(s) for s in range(2, 15)] + ['J'+str(s) for s in range(2, 15)] + ['W', 'J']
for k in cards:
for pos in range(n_players):
stats[k+'-'+str(pos)] = []
# Run simulation
for _ in range(n_games):
w, trump_card, player_cards = play_game(n_players)
# Populate stats dictionary with output of the game
for pos, card in enumerate(player_cards):
if "-" in card:
card_n, card_s = card.split("-")
if trump_card is None:
istrump = 'J'
else:
istrump = 'T' if card_s == trump_card else ''
else:
card_n = card # Wizard or Jester
istrump = ''
if pos == w:
stats[istrump+card_n+'-'+str(pos)].append(1) # win
else:
stats[istrump+card_n+'-'+str(pos)].append(0) # lossThe stats dictionary now contains the results of the games for each card and player. So stats['T2-3'] is a list of 0 and 1 representing whether the third player won or lost while holding a 2 from the trump suit.
Finally, we will concatenate the results of the simulation in a table which will summarize the expected value of the number of points the player will receive if betting 1 for the first round (=betting that the player wins the trick).
# Concatenate all stats into a dataframe of results
df = pd.DataFrame(0, index=cards_n, columns=[str(pos) for pos in range(n_players)])
for k, v in stats.items():
n, pos = k.split("-")
df.loc[n, pos] = np.round(np.mean(v), 3)
# Expected Value if betting you win the trick
ev = df*30 - (1-df)*10
ev.columns = range(1, n_players+1)
ev.columns.name = "Position"
ev.index.name = "Card"Final results for 3 players of the expected value of the number of points the player will get if betting 1:
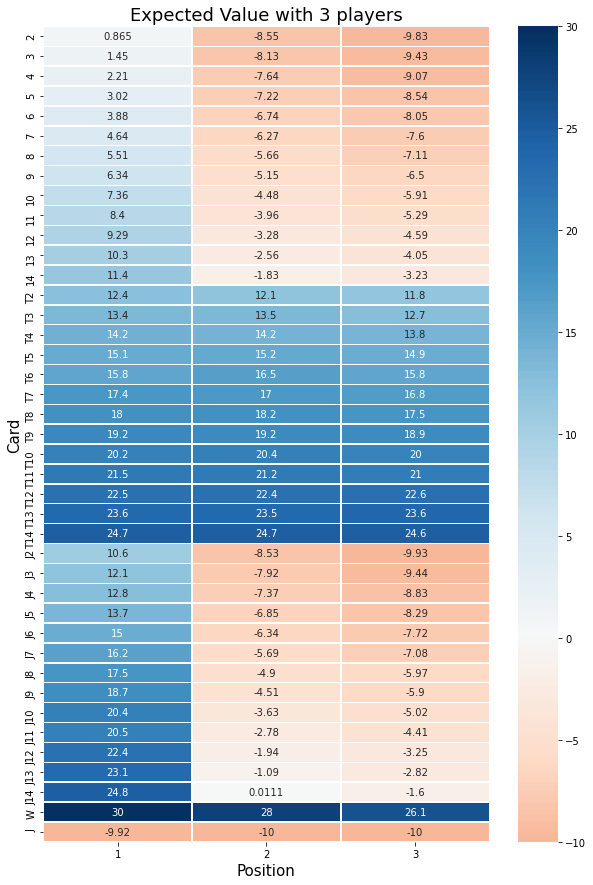
For 4 players:
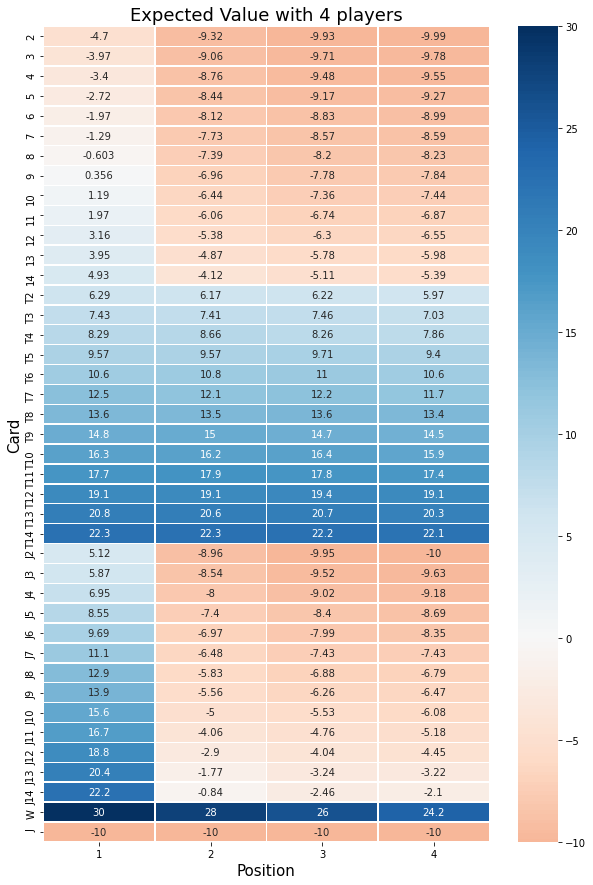
For 5 players:
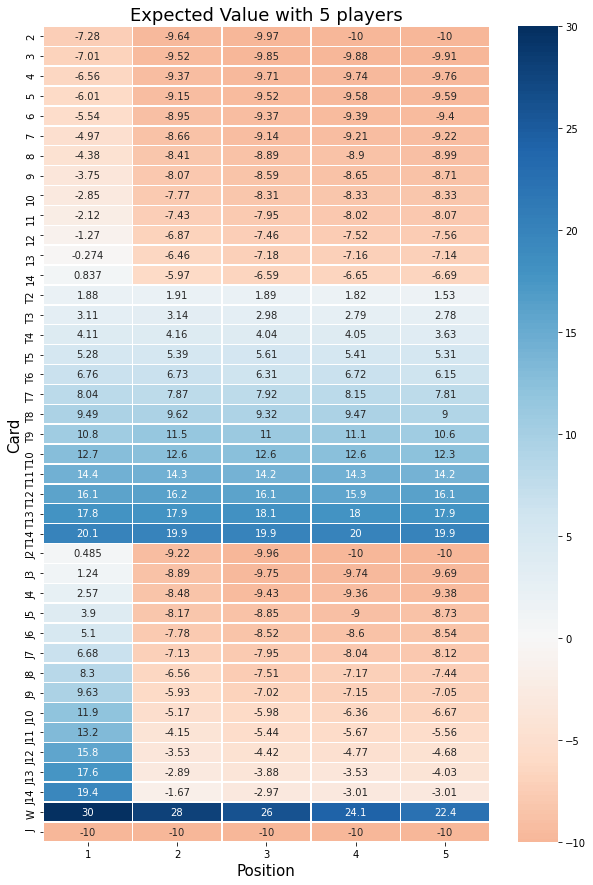
For 6 players:
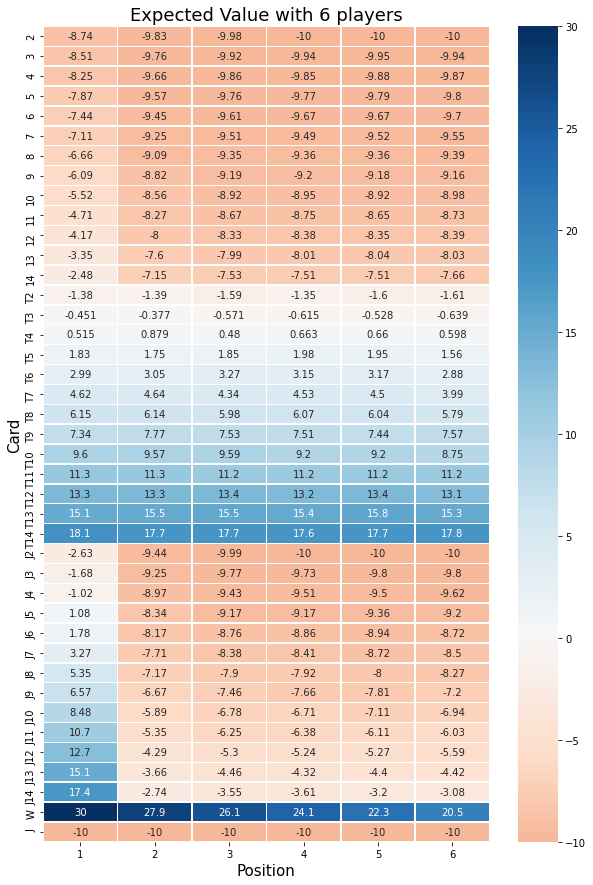
Sanity check
Let's try to calculate by hand one of these values to check our results. Let's compute the winning probability for T9-1: the first player holds the 9 of the trump suit. And let's assume we have 5 players. Per the table above, the expected value is 10.8.
There are 3 possibilities for this situation to arise:
- Card flipped is a same suit as first player's card and between 2 and 8.
- Card flipped is a same suit as first player's card and between 10 and 14 (=Ace).
- Card flipped is a Wizard and dealer chose the suit of the first player's card.
There are 60 cards in a game of Wizard.
- Situation 1 happens with probability 7/60.
- Situation 2 happens with probability 5/60.
- Situation 3 happens with probability 1/60 (we have probability of 4/60 for a Wizard to be flipped and then 1/4 probablity for the suit chosen to match the first player's so total is 1/60).
How many cards are better than the player's card?
- In the first situation, there are 9 cards better than the player's (4 Wizards + 5 trump cards).
- In the second situation, there are 8 cards better than the player's (4 Wizards + 4 trump cards).
- In the third situation, there are 8 cards better than the player's (3 Wizards + 5 trump cards).
How many cards are worse than the player's card?
- In the first situation, there are 49 cards worse than the player's (there are 58 cards remaining in the deck other than the player's card and the card flipped by the dealer so 58 - 9 = 49).
- In the second situation, there are 50 cards worse than the player's.
- In the third situation, there are 50 cards worse than the player's.
How many possibilities for the other 4 players to have a worse card than the player's?
- In the first situation, we have \({{49 \choose 4}}\) combinations.
- In the second situation, we have \({{50 \choose 4}}\) combinations.
- In the third situation, we have \({{50 \choose 4}}\) combinations.
Finally, it gives us the following winning probability for T9-1:
\[p(T9-1) = \frac{{49 \choose 4}}{{58 \choose 4}} \frac{\frac{7}{60}}{\frac{13}{60}} + \frac{{50 \choose 4}}{{58 \choose 4}} \frac{\frac{5}{60}}{\frac{13}{60}} + \frac{{49 \choose 4}}{{58 \choose 4}} \frac{\frac{1}{60}}{\frac{13}{60}}\]
\[p(T9-1) = 0.519\]
As a result, the expected value for the number of points won:
\[EV = p(T9-1) * 30 - (1-p(T9-1)) * 10\]
\[EV = 10.78 \]
Which is very close to the value found with our Monte Carlo simulation.
Conclusion
Based on the results above, below are the rules one should follow in the first round of Wizard to maximise winning probablities:
- If a player holds a Wizard, bet 1
- If a player holds a Jester, bet 0
- If there is a trump suit:
- The FIRST player should bet 1.
- ... unless there are 4 players then bet 1 only if holding a trump card or a non trump card of at least 9, otherwise 0.
- ... unless there are 5 players then bet 1 only if holding a trump card or a non trump card of at least an ace, otherwise 0.
- ... unless there are 6 players then bet 1 only if holding a trump card of at least 4, otherwise 0.
- OTHER players should bet 1 if they have a trump card, otherwise 0.
- unless there are 6 players then then bet 1 only if the card is at least a 4.
- The FIRST player should bet 1.
- If there are NO trump suit (=Jester flipped by the dealer):
- The FIRST player should bet 1.
- ... unless there are 6 players then bet 1 only if the card is at least a 5.
- OTHER players should always bet 0.
- The FIRST player should bet 1.